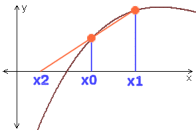
 When solving f(x) = 0 \, in situations where the derivative f'(x) of a function is difficult to find, the Newton-Raphson method will be inappropriate. This problem can be overcome by approximating the derivative. In this case we will need two approximations x_0 and x_1 to the root of the equation f(x)=0 \,. The line through (x_0, f(x_0)) and (x_1, f(x_1)) is called a secant and where it crosses the x-axis is taken as our next approximation, x_2, to the root.
When solving f(x) = 0 \, in situations where the derivative f'(x) of a function is difficult to find, the Newton-Raphson method will be inappropriate. This problem can be overcome by approximating the derivative. In this case we will need two approximations x_0 and x_1 to the root of the equation f(x)=0 \,. The line through (x_0, f(x_0)) and (x_1, f(x_1)) is called a secant and where it crosses the x-axis is taken as our next approximation, x_2, to the root.
This root can be found using: x_{2} = \displaystyle \frac{x_0f(x_1)- x_1f(x_0)}{f(x_1)-f(x_0)}
This applet demonstrates finding a the root of a function f(x) by the Secant Algorithm. How well this method works depends on how well we choose the initial two points.
To run the demo:
- Choose a function.
- Click the mouse on the graph along the x axis to pick the two starting points. For the best results, the second point should be closer to the root.
- Press the Step button to single-step the algorithm.
- Press the Run button to animate the algorithm.
Summary/Background
The secant method does not require that the root remain bracketed and hence it does not always converge. The false position method uses the same formula as the secant method but always converges because it requires x_1 and x_2 to be either side of the root.
Software/Applets used on this page

This applet forms part of "Java Number Cruncher: The Java Programmer's Guide to Numerical Computation", Prentice-Hall, by Ronald Mak, and is provided for MathsNetAlevel-plus by that author - see
Apropos-logic
Apropos-logic
This question appears in the following syllabi:
| Syllabus | Module | Section | Topic | Exam Year |
|---|---|---|---|---|
| OCR-MEI A-Level (UK - Pre-2017) | NM | Numerical Methods | The secant method | - |
| Universal (all site questions) | N | Numerical Methods | The secant method | - |
